Tugas 7 Teori Bahasa dan Automata - Finite State Automata & Non Finite State Automata
Luky Mulana (1810631170200) 4G - Dalam postingan saya akan membahas materi tentang Finite State Automata & Non Finite State Automata. Terdapat 5 point yang akan dibahas, yaitu :
1. Penerapan FSA
Dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima. Deterministik artinya tertentu/sudah tertentu fungsi transisinya.
Notasi matematis DFA:
M = (Q, S, d, q0, F)
Contoh : Pengujian untuk menerima bit string dengan banyaknya 0 genap, serta banyaknya 1 genap.
0011 : diterima
10010 : ditolak, karena banyaknya 0 ganjil
Diagram transisi-nya :
DFA nya:
Q = {q0 , q1 , q2 , q3 }
Σ = {0,1}
S = q0
F = { q0}
fungsi transisi adalah:
δ( q0,011)= δ( q2,11) =δ( q3,1)= q2 (Ditolak)
δ( q0,1010)= δ( q1,010) =δ( q3,10)=δ( q2,0)= q0 (Diterima)
3. NFA(non deterministik Finite Automata)
- Penerapan FSA
- DFA(Deterministik Finite Automata)
- NFA(non deterministik Finite Automata)
- Ekuivalen antar DFA
- Reduksi Jumlah State pada FSA
Untuk lebih jelasnya saya akan menjelaskan setiap point pada penjelasanya dibawah ini.
1. Penerapan FSA
Finite State Automata (FSA) adalah model matematika yang dapat menerima input dan mengeluarkan output yang memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke state lainnya berdasarkan input dan fungsi transisi. Finite state automata tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.
Finite State Automata dinyatakan oleh pasangan 5 tuple, yaitu:
Q = himpunan state
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q
Finite Automata memiliki beberapa karakteristik diantaranya :
Setiap Finite State Automata juga memiliki :
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q
Finite Automata memiliki beberapa karakteristik diantaranya :
- Setiap Finite Automata memiliki keadaan dan transisi yang terbatas.
- Transisi dari satu keadaan ke keadaan lainnya dapat bersifat deterministik atau non-deterministik.
- Setiap Finite Automata selalu memiliki keadaan awal.
- Finite Automata dapat memiliki lebih dari satu keadaan akhir jika setelah pemrosesan seluruh string, keadaan akhir dicapai, artinya otomata menerima string tersebut.
- Himpunan berhingga (finite) status (state)
- Himpunan berhingga simbol masukan
- Fungsi transisi
Cara Kerja Finite State Automata
Finite State Automata bekerja dengan cara mesin membaca memori masukan berupa tape yaitu 1 karakter tiap saat (dari kiri ke kanan) menggunakan head baca yang dikendalikan oleh kotak kendali state berhingga dimana pada mesin terdapat sejumlah state berhingga.
Finite Automata selalu dalam kondisi yang disebut state awal (initial state) pada saat Finite Automata mulai membaca tape. Perubahan state terjadi pada mesin ketika sebuah karakter berikutnya dibaca. Ketika head telah sampai pada akhir tape dan kondisi yang ditemui adalah state akhir, maka string yang terdapat pada tape dikatakan diterima Finite Automata (String-string merupakan milik bahasa bila diterima Finite Automata bahasa tersebut).
Penerapan
Secara formal FSA atau AH (Automata Hingga) dapat didefinisikan sebagai pasangan 5 Tupel atau TUPLE-5 : (K, VT, M, S, Z) atau M(inisial Tuple) = (Q, ∑, δ, S, F).
Dimana :
K atau Q : himpunan hingga stata,
VT atau ∑ (Sigma) : himpunan hingga simbol input (alfabet)
M atau δ (Delta) : fungsi transisi, menggambarkan transisi stata AH akibat pembacaan simbol input. (Fungsi transisi ini biasanya diberikan dalam bentuk tabel.)
S ∈ K atau S ∈ Q : stata AWAL
Z ⊆ K atau F ⊆ Q : himpunan stata penerima atau AKHIR
Finite State Diagram (FSD)
Finite State Automata dapat dimodelkan dengan Finite State Diagram (FSD) dapat juga disebut State Transition Diagram. Sistem transisi adalah sistem yang tingkah lakunya disajikan dalam bentuk keadaan-keadaan (states). Sistem tersebut dapat bergerak dari state yang satu ke state lainnya sesuai dengan input yang diberikan padanya.
Finite State Diagram terdiri dari:
1. Lingkaran menyatakan state
Lingkaran diberi label sesuai dengan nama state tersebut. Adapun pembagian lingkaran adalah:
· Lingkaran bergaris tunggal berarti state sementara
· Lingkaran bergaris ganda berarti state akhir
2. Anak Panah menyatakan transisi yang terjadi.
Label di anak panah menyatakan simbol yang membuat transisi dari 1 state ke state lain. 1 anak panah diberi label start untuk menyatakan awal mula transisi dilakukan.
Contoh FSA : pengecekan pariti ganjil
Misal input : 1101
Genap 1 Ganjil 1 Genap 0 Genap 1 Ganjil : diterima mesin
Misal input : 1100
Genap 1 Ganjil 1 Genap 0 Genap 0 Genap : ditolak mesin
Dari contoh diatas, maka:
Q = {Genap, Ganjil}
Σ = {0,1}
S = Genap
F = {Ganjil }
atau
δ(Genap,0) = Genap
δ(Genap,1) = Ganjil
δ(Ganjil,0) = Ganjil
δ(Ganjil,1) = Genap
Sebuah FSA dibentuk dari lingkaran yang menyatakan state:
· Label pada lingkaran adalah nama state
· Busur menyatakan transisi/ perpindahan
· Label pada busur yaitu symbol input
· Lingkaran yang didahului sebuah busur tanpa label menyatakan state awal
· Lingkaranb ganda menyatakan state akhir/ final.
Jadi sebuah mesin otomata dapat dinyatakan dalam diagram transisi, fungsi transisi dan tabel transisi.
FSA terbagi menjadi dua jenis, yaitu :
1. Deterministic Finite Automata
Artinya: Dari suatu state ada tepat satu state berikutnya untuk setiap simbol input yang diterima.
2. Non Deterministic Finite Automata (NDFA) / NFA
Artinya: Dari suatu state bisa terdapat 0,1 atau lebih busur keluar (transisi) berlabel simbol input yang sama.
2. DFA(Deterministik Finite Automata)
Notasi matematis DFA:
- M = nama DFA
- Q = himpunan keadaan DFA
- S = himpunan alfabet
- d = fungsi transisi
- q0 = keadaan awal
- F = keadaan akhir
M = (Q, S, d, q0, F)
Contoh : Pengujian untuk menerima bit string dengan banyaknya 0 genap, serta banyaknya 1 genap.
0011 : diterima
10010 : ditolak, karena banyaknya 0 ganjil
Diagram transisi-nya :
Q = {q0 , q1 , q2 , q3 }
Σ = {0,1}
S = q0
F = { q0}
fungsi transisi adalah:
δ( q0,011)= δ( q2,11) =δ( q3,1)= q2 (Ditolak)
δ( q0,1010)= δ( q1,010) =δ( q3,10)=δ( q2,0)= q0 (Diterima)
3. NFA(non deterministik Finite Automata)
Non Deterministic Finite Automata (NFA) → M = (Q, ∑, δ, S, F), dimana :
Q : Himpunan state/kedudukan
∑ (Sigma) : Himpunan simbol input
δ (Delta) : Fungsi transisi, dimana δ ∈ Q x (∑ ⋃ ε) → P(Q)
P(Q) : set of all subsets of Q
S ∈ : State awal (initial state)
F ⊆ : Himpunan state akhir (final state)
Language → L(M) : (x | δ (S,x) di dalam F)
Dari suatu state ada 0, 1 atau lebih state berikutnya untuk setiap simbol masukan yang diterima. Non-Deterministic Finite Automata:
- Otomata berhingga yang tidak pasti untuk setiap pasangan state input, bisa memiliki 0 (nol) atau lebih pilihan untuk state berikutnya.
- Untuk setiap state tidak selalu tepat ada satu state berikutnya untuk setiap simbol input yang ada.
- Dari suatu state bisa terdapat 0,1 atau lebih busur keluar (transisi) berlabel simbol input yang sama.
- Untuk NFA harus dicoba semua kemungkinan yang ada sampai terdapat satu yang mencapai state akhir.
- Suatu string x dinyatakan diterima oleh bahasa NFA, M= (Q, _, d, S, F) bila {x | d (S,x) memuat sebuah state di dalam F}
Kedua finite automata di atas mampu mengenali himpunan reguler secara presisi. Dengan demikian kedua finite automata itu dapat mengenali string-string yang ditunjukkan dengan ekspresi reguler secara tepat. DFA dapat menuntun recognizer(pengenal) lebih cepat dibanding NDFA. Namun demikian, DFA berukuran lebih besar dibanding NDFA yang ekivalen dengannya. Lebih mudah membangun NDFA dibanding DFA untuk suatu bahasa, namun lebih mudah mengimplementasikan DFA dibanding NDFA.
Contoh :
NFA (Q, ∑, δ, S, F). dimana :
Q = {q 0, q1 , q2 ,q3 , q4 }
δ diberikan dalam tabel berikut :
∑= {a, b,c}
S = q0
F = {q4}
Diagram atau Graf yang dapat dibuat :
L(M) = {aaa, ..., abab, ..., acbc, ...}
4. Ekuivalen antar DFA
Untuk suatu bahasa regular, kemungkinan ada sejumlah Deterministic Finite Automata yang dapat menerimanya. Perbedaannya hanyalah jumlah state yang dimiliki otomata-otomata yang saling ekuivalen tersebut. Tentu saja, dengan alasan kepraktisan, kita memilih otomata dengan jumlah state yang lebih sedikit.
Sasaran kita di sini adalah mengurangi jumlah state dari suatu Finite State Automata, dengan tidak mengurangi kemampuannya semula untuk menerima suatu bahasa.
Ada dua buah istilah baru yang perlu kita ketahui yaitu :
1. Distinguishable yang berarti dapat dibedakan.
2. Indistinguishable yang berarti tidak dapat dibedakan.
Dua DFA M1 dan M2 dinyatakan ekivalen apabila L(M1) = L(M2)
5. Reduksi Jumlah State pada FSA
Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi). State pada FSA dapat direduksi apabila terdapat useless state. Hasil dari FSA yang direduksi merupakan ekuivalensi dari FSA semula.
Pasangan State dapat dikelompokkan berdasarkan:
Distinguishable State yang artinya dapat dibedakan. Dua state p dan q dari suatu DFA dikatakan indistinguishable apabila : δ(q,w) ∈ F dan δ(p,w) ∈ F atau δ(q,w) ∉ F dan δ(q,w) ∉ F
Indistinguishable State yang artinya tidak dapat dibedakan. Dua state p dan q dari suatu DFA dikatakan distinguishable apabila : Ada string w ∈ S* hingga δ(q,w) ∈ F dan δ(p,w) ∉ F
Relasi :
Pasangan dua buah state memiliki salah satu kemungkinan : distinguishable atau indistinguishable tetapi tidak kedua-duanya.
Dalam hal ini terdapat sebuah relasi :
Jika p dan q indistinguishable,
dan q dan r indistinguishable
maka p, r indistinguishable
dan p,q,r indistinguishable
Dalam melakukan eveluasi state, didefinisikan suatu relasi :
Untuk Q yg merupakan himpunan semua state
- D adalah himpunan state-state distinguishable, dimana D Ì Q
- N adalah himpunan state-state indistinguishable, dimana N Ì maka x Î N jika x Î Q dan x ∉ D
Langkah :
- Hapuslah semua state yg tidak dapat dicapai dari state awal (useless state)
- Buatlah semua pasangan state (p, q) yang distinguishable, dimana p ∈ F dan q ∉F. Catat semua pasangan-pasangan state tersebut.
- Cari state lain yang distinguishable dengan aturan: “Untuk semua (p, q) dan semua a ∈ ∑, hitunglah δ (p, a) = pa dan δ (q, a) = qa” Jika pasangan (pa, qa) adalah pasangan state yang distinguishable maka pasangan (p, q) juga termasuk pasangan yang distinguishable.
- Semua pasangan state yang tidak termasuk sebagai state yang distinguishable merupakanstate-state indistinguishable.
- Beberapa state yang indistinguishable dapat digabungkan menjadi satu state.
- Sesuaikan transisi dari state-state gabungan tersebut.
Contoh :
Lakukan Reduksi State pada DFA di atas?
Jawab :
Langkah :
1. State q5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state). Hapus state q5.
2. Catat state-state distinguishable, yaitu :
q4 ∈ F sedang q0, q1, q2, q3 ∉F sehingga pasangan
(q0, q4) (q1, q4) (q2, q4) dan (q3, q4) adalah distinguishable.
3. Pasangan-pasangan state lain yang distinguishable diturunkan berdasarkan pasangan dari langkah kedua, yaitu :
- Untuk pasangan (q0, q1)
δ(q0, 0) = q1 dan δ(q1, 0) = q2 → belum teridentifikasi
δ(q0, 1) = q3 dan δ(q1, 1) = q4 → (q3, q4) distinguishable
maka (q0, q1) adalah distinguishable.
- Untuk pasangan (q0, q2)
δ(q0, 0) = q1 dan δ(q2, 0) = q1 → belum teridentifikasi
δ(q0, 1) = q3 dan δ(q2, 1) = q4 → (q3, q4) distinguishable
maka (q0, q2) adalah distinguishable.
4. Setelah diperiksa semua pasangan state maka terdapat state-state yang distinguishable : (q0,q1), (q0,q2), (q0,q3), (q0,q4), (q1,q4), (q2,q4), (q3,q4) Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q1, q2), (q1, q3) dan (q2, q3) distinguishable, sehingga disimpulkan pasangan-pasangan state tersebut indistinguishable.
5. Karena q1 indistinguishable dengan q2, q2 indistinguishable dengan q3, maka dapat disimpulkan q1, q2, q3 saling indistinguishable dan dapat dijadikan satu state.
6. Berdasarkan hasil diatas makahasil dari DFA yang direduksi menjadi :
Daftar Pustaka
- Materi 7 Finite State Automata & Non Finite State Automata [pdf]. Dosen Pengampu: Garno, M.Kom. Fakultas Ilmu Komputer, Universitas Singaperbangsa Karawang.
- https://docplayer.info/36555908-Teori-bahasa-dan-automata-finite-state-automata-non-finite-state-automata.html
- https://riskasimaremare.wordpress.com/2013/04/23/finite-state-automata/
- https://www.slideshare.net/ahmadhaidaroh/materi-3-finite-state-automata
Tugas 6 Teori Bahasa dan Automata - Tata Bahasa Bebas Konteks (Pohon Penurunan)
Parsing
Sebuah pohon (tree) adalah suatu graph terhubung tidak sirkuler, yang memiliki satu simpul (node) / vertex disebut akar (root) dan dari situ memiliki lintasan ke setiap simpul. Pohon sintaks / pohon penurunan (syntax tree/derivaton tree/parse tree) berguna untuk menggambarkan bagaimana memperoleh suatu string (untai) dengan cara menurunkan simbol-simbol variabel menjadi simbol-simbol terminal. Setiap simbol variabel diturunkan menjadi terminal, sampai tidak ada yang belum tergantikan.
Contoh :
S → AB
A → aA | a
B → bB | b
Untai yang dicari: aabbb . Maka Pohon Penurunannya:
Proses penurunan atau parsing bisa dilakukan dengan cara:
1. Penurunan terkiri (leftmost derivation):
Setiap tahapan penurunan variabel / non terminal terkiri yang diuraikan .
Symbol variabel terkiri yang diperluas terlebih dahulu.
2. Penurunan terkanan (right derivation):
Setiap tahapan penurunan variabel / non terminal paling kanan yang diuraikan.
Symbol variabel terkanan yang diperluas terlebih dahulu.
Misal, terdapat tata bahasa bebas konteks:
S → aAS | a
A → SbA | ba
Untuk memperoleh untai ‘aabbaa’ :
Dengan penurunan terkiri:
S → aAS → aSbAS → aabAS → aabbaS → aabbaa
Dengan penurunan terkanan :
S → aAS → aAa → aSbAa → aSbbaa → aabbaa
Meskipun proses penurunan berbeda, namun akan tetap memiliki pohon penurunan yang sama. Maka Pohon Penurunannya:
Ambiguitas
Terjadi bila terdapat lebih dari satu pohon penurunan yang berbeda utuk memperoleh suatu untai.
Misal terdapat tata bahasa bebas konteks:
S → SbS | ScS | a
Untuk memperoleh untai ‘abaca’.
Cara pertama:
S → SbS → SbScS → SbSca → Sbaca → abaca
Cara kedua:
S → ScS → SbScS → abScS → abacS → abaca
Latihan Soal
Soal 1
Terdapat tata bahasa bebas konteks:
S → AA
A → AAA | a | bA | Ab
Maka untuk memperoleh untai " bbabaaba " adalah sebagai berikut:
- Penurunan Terkiri
S → AA → bAA → bbAA → bbAbA → bbabA →bbabAAA → bbabaaA → bbabaabA → bbabaaba
Soal 2
Terdapat tata bahasa bebas konteks:
S → AB
A → Aa | bB
B → a | Sb
Maka untuk memperoleh untai " baabaab " adalah sebagai berikut:
- Penurunan Terkiri
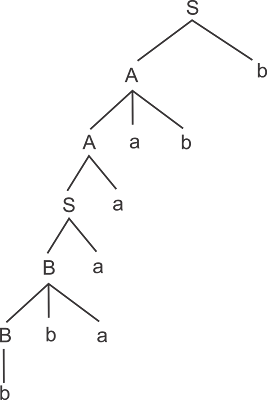
S → AB→ AaB→ bBaB→ baaB → baaSb → baaABb → baabBBb → baabaBb→ baabaab
- Pohon Penurunan
Soal 3
Terdapat tata bahasa bebas konteks:
S → Ba | Ab
A → Sa | Aab | a
B → Sb | Bba | b
Maka untuk memperoleh untai " bbaaaabb " adalah sebagai berikut:
- Penurunan Terkiri :
S → Ab→ Aabb→ Saabb→ Baaabb→ Bbaaaabb → bbaaaabb
- Pohon Penurunan
Soal 4 (Ambiguitas)
Terdapat tata bahasa bebas konteks (Ambiguitas):
S → AB | C
A → aAb | ab
B → cBd | cd
C → aCd | aDd
D → bDc | bc
Maka terdapat 2 untai " aabbccdd " adalah sebagai berikut:
Karena soal diatas adalah ambiguitas maka terdapat dua penurunan yaitu :
- S → AB
- S → C
Penurunan Terkiri dari S → AB adalah :
S → AB→ aAbB→ aabbB→ aabbcBd→ aabbccdd
Pohon Penurunanya adalah :
Penurunan Terkiri dari S → C adalah :
S → C→ aCd→ aaDdd→ aabDcdd→ aabbccdd
Pohon Penurunannya adalah :
Untuk lebih jelasnya saya menjelaskan lewat media berupa video dan bisa ditonton dibawah ini.
- https://www.academia.edu/8702157/20120515_Teori_Bahasadan_Otomata_TBO_-Pohon_Penurunan
- http://apranolo.tif.uad.ac.id/wp-content/uploads/2014/12/TBA_TID_Kelompok-7_TATA-BAHASA-BEBAS-KONTEKS.pdf
- Materi 6 Tata Bahasa Bebas Konteks (Pohon Penurunan) [pdf]. Dosen Pengampu: Garno, M.Kom. Fakultas Ilmu Komputer, Universitas Singaperbangsa Karawang.
Tugas 5 Teori Bahasa dan Automata - Penyederhanaan Tata Bahasa Bebas Konteks
Luky Mulana (1810631170200) 4G - Tujuan penyederhanaan adalah untuk melakukan pembatasan sehingga tidak menghasilkan pohon penurunan yang memiliki kerumitan yang tidak perlu atau aturan produksi yang tidak berarti.
Langkah-langkah penyederhanaan dari tata bahasa bebas konteks ini adalah dengan cara sebagai berikut:
1. Penghilangkan Produksi Useless
2. Penghilangkan Produksi Unit
3. Penghilangkan Produksi Empty
Setiap teknik mempunyai caranya masing-masing, bagaimana caranya. Mari kita bahas satu persatu.
1. Penghilangan Produksi Useless
Produksi Useless adalah produksi yang memuat simbol variable yang tidak memiliki penurunan yang akan menghasilkan terminal-terminal seluruhnya dan produksi yang tidak akan pernah dicapai dengan penurunan apapun dari simbol awal, sehingga produk itu redudan.
Contoh:
Terdapat aturan produksi sebagai berikut :
S → aBD
B → cD | Ab
D → ef
A → Ed
F → dc
Penggunaan Produk Useless :
1. Aturan produksi A → Ed , E tidak memiliki penurunan. Sehingga dapat dihilangkan.
2. Aturan produksi F → dc, redudan. Sehingga aturan produksi tersebut dapat dihilangkan.
3. Aturan produksi B → Ab, A tidak memiliki penurunan. Sehingga dapat dihilangkan.
Maka hasil akhirnya:
S → aBD
B → cD
D → ef
2. Penghilangan Produksi Unit
Produksi Unit adalah produksi dimana ruas kiri dan kanan aturan produksi hanya berupa satu simbol variabel. Contoh A → B, atau C → D.
Contoh :
Diberikan aturan produksi sebagai berikut :
S → Sb
S → C
C → D
C → ef
D → dd
Penggunaan Produk Useless :
C → D => C → dd
S → C => S → dd | ef
Sehingga aturan produksi yang telah disederhanakan dengan menghilangkan produksi unit adalah sebagai berikut :
S → Sb
S → dd | ef
C → dd
C → ef
D → dd
3. Penghilangan Produksi Empty (ε)
Produksi Empty adalah produksi dalam bentuk α → ε atau bisa dianggap sebagai produksi kosong (empty). Penghilangan produksi empty dilakukan dengan melakukan penggantian produksi yang memuat variable ε, atau disebut juga Nullable.
Contoh :
Terdapat tata bahasa bebas konteks sebagai berikut :
S → aB | Cd
A → d
C → ε
Variabel yang nullable adalah variable C, karena penurunan C → ε merupakan penurunan satu-satunya dari C, maka kita ganti S → Cd menjadi S → d, kemudian produksi C → ε kita hapus.
Maka hasil penyederhanaannya adalah :
S → aB | d
A → d
Alur Penyederhanaan Tata Bahasa Bebas Konteks
Selanjutnya ada pembahasan mengenai soal latihan penyederhanaan tata bahasa bebas konteks. Dalam soal latihan tersebut akan dijabarkan pengerjaan dalam setiap teknik yang diguanakan dalam penyerderhanaan tata bahasa bebas konteks.
Soal Latihan
1. Penyederhanaan dengan penghilangan produksi useless
a. Soal Latihan 1
S → aB | C
B → e | Ab
C → bCb | adF | ab
F → cFB
Jawab :
Penghilangan Produksi Useless:
B → Ab (A tidak punya penurunan)
C → adF (F tidak punya penurunan)
F → cFB (F tidak punya penurunan ke terminal)
Hasil Penyederhanaan:
S → aB | C
B → e
C → bCb | ab
b. Soal Latihan 2
S → Aa | B
A → ab | D
B → b | E
C → bb
E → aEa
Jawab :
Penghilangan Produksi Useless:
A → D (A tidak punya penurunan)
B → E (F tidak punya penurunan)
C → bb (C → bb adalah redudan)
E → aEa (E tidak punya penurunan ke terminal)
Hasil Penyederhanaan:
S → Aa | B
A → ab
B → b
2. Penyederhanaan dengan penghilangan produksi unit
a. Soal Latihan 1
S → Aa | B
B → A | bb
A → a | bc | B
Jawab :
Penghilangan produksi unit:
A → B ==> A → bb
B → A ==> B → a | bc | bb , Karena B → bb sudah ada maka cukup B → a | bc
S → B ==> S → a | bc | bb
Hasil Penyederhanaan:
S → Aa | a | bc | bb
B → a | bc | bb
A → a | bc | bb
b. Soal Latihan 2
S → A | Aa
A→ B
B → C | b
C → D | ab
D → b
Jawab :
Penghilangan produksi unit:
C → D ==> C → b
B → C ==> B → b | ab , Karena B → b sudah ada maka cukup B → ab
A → B ==> A → ab | b
S → A ==> S → ab | b
Hasil Penyederhanaan:
S → ab | b | Aa
A → ab | b
B → ab | b
C → b | ab
D → b
3. Penyederhanaan dengan penghilangan produksi empty (ε)
a. Soal Latihan 1
S → AB
A → abB | aCa | ε
B → bA | BB | ε
C → ε
Jawab :
Penghilangan produksi empty(ε):
Variabel yang nullable: A,B,C, maka:
A → ε (dihapus)
Maka, S → AB | B
A → abB | ab | aa
B → b | BB
B → ε (dihapus)
Maka, S → AB | A
B → bA | BB | B
A → abB | ab | aa
C → ε (dihapus)
Maka, A → abB | aa
Hasil Penyederhanaan:
S → AB | A | B
A → abB | ab | aa
B → bA | b | BB | B
b. Soal Latihan 2
S → aBCD | bb | A | ε
A → CDa | ef
B → b | Af | ε
C → BbC | ea
D → ε
Jawab :
Penghilangan produksi empty(ε):
Variabel yang nullable: S,B,D, maka:
D → ε (dihapus)
Maka, A → CDa | ef ==> A → Ca | ef
S → aBCD | bb | A | ε ==> S → aBC | bb | A | ε
B → ε (dihapus)
Maka, C → BbC | ea ==> C → BbC | bC| ea
S → aBC | bb | A | ε ==> S → aBC | aC | bb | A | ε
S → ε (dihapus)
Maka, S → aBC | aC | bb | A
Hasil Penyederhanaan:
S → aBC | aC | bb | A
A → Ca | ef
B → b | Af
C → BbC | bC | ea
4. Latihan Kompleks
Lakukan penyederhanaan pada himpunan produksi berikut dengan penghilangan empty + unit + useless sekaligus.
S → BACa
B → AC
A → dC | ε
C → D | ε
D → d
Jawab :
• Penghilangan produksi empty(ε):
Variabel yang nullable: A,C, maka:
A → ε (dihapus)
C → ε (dihapus)
Maka:
S → BACa |BAa | BCa
B → AC | A | C
A → dC | d
C → D
D → d
• Penghilangan produksi unit:
C → D ==> C → d
B → A ==> B → dC | d
B → C ==> B → d
Maka:
S → BACa |BAa | BCa
B → AC | dC | d
A → dC | d
C → d
D → d
• Penghilangan produksi useless:
D → d (D → d adalah redudan)
• Hasil Akhir Penyederhanaan:
S → BACa |BAa | BCa
B → AC | dC | d
A → dC | d
C → d
Untuk lebih jelasnya, saya menguraikan penjelasan soal latihan diatas menjadi video.
Contoh:
Terdapat aturan produksi sebagai berikut :
S → aBD
B → cD | Ab
D → ef
A → Ed
F → dc
Penggunaan Produk Useless :
1. Aturan produksi A → Ed , E tidak memiliki penurunan. Sehingga dapat dihilangkan.
2. Aturan produksi F → dc, redudan. Sehingga aturan produksi tersebut dapat dihilangkan.
3. Aturan produksi B → Ab, A tidak memiliki penurunan. Sehingga dapat dihilangkan.
Maka hasil akhirnya:
S → aBD
B → cD
D → ef
2. Penghilangan Produksi Unit
Produksi Unit adalah produksi dimana ruas kiri dan kanan aturan produksi hanya berupa satu simbol variabel. Contoh A → B, atau C → D.
Contoh :
Diberikan aturan produksi sebagai berikut :
S → Sb
S → C
C → D
C → ef
D → dd
Penggunaan Produk Useless :
C → D => C → dd
S → C => S → dd | ef
Sehingga aturan produksi yang telah disederhanakan dengan menghilangkan produksi unit adalah sebagai berikut :
S → Sb
S → dd | ef
C → dd
C → ef
D → dd
3. Penghilangan Produksi Empty (ε)
Produksi Empty adalah produksi dalam bentuk α → ε atau bisa dianggap sebagai produksi kosong (empty). Penghilangan produksi empty dilakukan dengan melakukan penggantian produksi yang memuat variable ε, atau disebut juga Nullable.
Contoh :
Terdapat tata bahasa bebas konteks sebagai berikut :
S → aB | Cd
A → d
C → ε
Variabel yang nullable adalah variable C, karena penurunan C → ε merupakan penurunan satu-satunya dari C, maka kita ganti S → Cd menjadi S → d, kemudian produksi C → ε kita hapus.
Maka hasil penyederhanaannya adalah :
S → aB | d
A → d
Alur Penyederhanaan Tata Bahasa Bebas Konteks
Selanjutnya ada pembahasan mengenai soal latihan penyederhanaan tata bahasa bebas konteks. Dalam soal latihan tersebut akan dijabarkan pengerjaan dalam setiap teknik yang diguanakan dalam penyerderhanaan tata bahasa bebas konteks.
Soal Latihan
1. Penyederhanaan dengan penghilangan produksi useless
a. Soal Latihan 1
S → aB | C
B → e | Ab
C → bCb | adF | ab
F → cFB
Jawab :
Penghilangan Produksi Useless:
B → Ab (A tidak punya penurunan)
C → adF (F tidak punya penurunan)
F → cFB (F tidak punya penurunan ke terminal)
Hasil Penyederhanaan:
S → aB | C
B → e
C → bCb | ab
b. Soal Latihan 2
S → Aa | B
A → ab | D
B → b | E
C → bb
E → aEa
Jawab :
Penghilangan Produksi Useless:
A → D (A tidak punya penurunan)
B → E (F tidak punya penurunan)
C → bb (C → bb adalah redudan)
E → aEa (E tidak punya penurunan ke terminal)
Hasil Penyederhanaan:
S → Aa | B
A → ab
B → b
2. Penyederhanaan dengan penghilangan produksi unit
a. Soal Latihan 1
S → Aa | B
B → A | bb
A → a | bc | B
Jawab :
Penghilangan produksi unit:
A → B ==> A → bb
B → A ==> B → a | bc | bb , Karena B → bb sudah ada maka cukup B → a | bc
S → B ==> S → a | bc | bb
Hasil Penyederhanaan:
S → Aa | a | bc | bb
B → a | bc | bb
A → a | bc | bb
b. Soal Latihan 2
S → A | Aa
A→ B
B → C | b
C → D | ab
D → b
Jawab :
Penghilangan produksi unit:
C → D ==> C → b
B → C ==> B → b | ab , Karena B → b sudah ada maka cukup B → ab
A → B ==> A → ab | b
S → A ==> S → ab | b
Hasil Penyederhanaan:
S → ab | b | Aa
A → ab | b
B → ab | b
C → b | ab
D → b
3. Penyederhanaan dengan penghilangan produksi empty (ε)
a. Soal Latihan 1
S → AB
A → abB | aCa | ε
B → bA | BB | ε
C → ε
Jawab :
Penghilangan produksi empty(ε):
Variabel yang nullable: A,B,C, maka:
A → ε (dihapus)
Maka, S → AB | B
A → abB | ab | aa
B → b | BB
B → ε (dihapus)
Maka, S → AB | A
B → bA | BB | B
A → abB | ab | aa
C → ε (dihapus)
Maka, A → abB | aa
Hasil Penyederhanaan:
S → AB | A | B
A → abB | ab | aa
B → bA | b | BB | B
b. Soal Latihan 2
S → aBCD | bb | A | ε
A → CDa | ef
B → b | Af | ε
C → BbC | ea
D → ε
Jawab :
Penghilangan produksi empty(ε):
Variabel yang nullable: S,B,D, maka:
D → ε (dihapus)
Maka, A → CDa | ef ==> A → Ca | ef
S → aBCD | bb | A | ε ==> S → aBC | bb | A | ε
B → ε (dihapus)
Maka, C → BbC | ea ==> C → BbC | bC| ea
S → aBC | bb | A | ε ==> S → aBC | aC | bb | A | ε
S → ε (dihapus)
Maka, S → aBC | aC | bb | A
Hasil Penyederhanaan:
S → aBC | aC | bb | A
A → Ca | ef
B → b | Af
C → BbC | bC | ea
4. Latihan Kompleks
Lakukan penyederhanaan pada himpunan produksi berikut dengan penghilangan empty + unit + useless sekaligus.
S → BACa
B → AC
A → dC | ε
C → D | ε
D → d
Jawab :
• Penghilangan produksi empty(ε):
Variabel yang nullable: A,C, maka:
A → ε (dihapus)
C → ε (dihapus)
Maka:
S → BACa |BAa | BCa
B → AC | A | C
A → dC | d
C → D
D → d
• Penghilangan produksi unit:
C → D ==> C → d
B → A ==> B → dC | d
B → C ==> B → d
Maka:
S → BACa |BAa | BCa
B → AC | dC | d
A → dC | d
C → d
D → d
• Penghilangan produksi useless:
D → d (D → d adalah redudan)
• Hasil Akhir Penyederhanaan:
S → BACa |BAa | BCa
B → AC | dC | d
A → dC | d
C → d
Untuk lebih jelasnya, saya menguraikan penjelasan soal latihan diatas menjadi video.
Subscribe to:
Comments
(
Atom
)